Modeling Technology Evolution

The Exponential Development of Technology

Ray Kurzweil has an idea that technology is driving technology itself forward. He named this idea The Law of Accelerating Returns ¹.

To indulge the readers, we build a mathematical model based on Kurzweil’s assumption. We assume a quantity $N(t)$ that describes the level of technology at time $t$. The amount of incremental of technology at time $t$ is proportional to a function of the amount of technology we have at time $t$,

$$ \begin{equation} \frac{\mathrm d N(t)}{\mathrm dt} = C\cdot f(N(t)), \end{equation} $$

where $C$ is a constant. The simplest choice for $f(N(t))$ is $N(t)$ itself. This leads to the equation

$$ \begin{equation} \frac{\mathrm d N(t)}{\mathrm dt} = C\cdot N(t). \end{equation} $$

The solution to the above equation is

$$ N(t) = \exp\left( C t \right) + N(t=-\infty). $$

The solution says that the level of technology is growing exponentially.

How do we verify this? The first idea came to me is through the number of patents. Since different countries built their own pattern system in different area in history, we will look at this country by country. The first country we look into is the United States. The data can be found at WIPO IP Statistics Data Center.

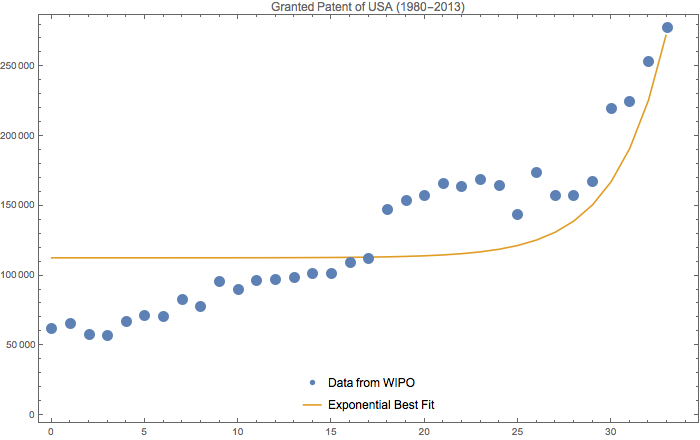
The above figure shows the granted patent in the USA during 1980-2013. The naively fitting formula is $e^{0.36 t}+1.13\times 10^5$, ignoring the disruptions in the society.

As an comparison, we also fit the data for China.

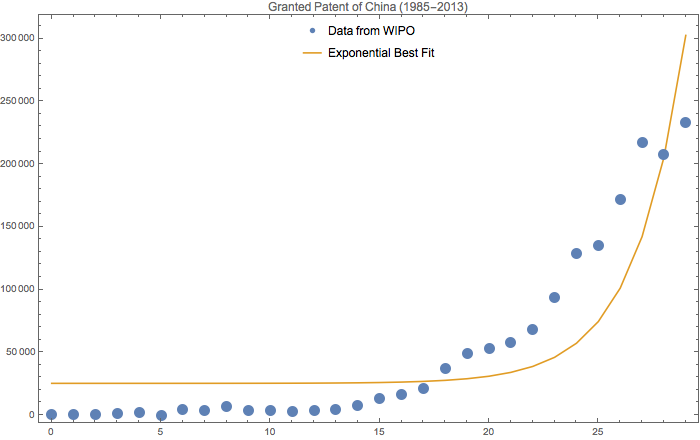
The above figure shows the granted patent in China during 1985-2013. The naive fitting formula is $e^{0.43 t}+2.53\times 10^4$. Again, we ignore all sorts of technologies of disruptions.

Modeling Destruction and Everything Else

Well, you could say the model doesn’t fit the data very well. This is pretty much expected. What we have been talking about is an ideal society for technology. In reality, policies, conflicts, and demographics have a lot of effects on the growth of society. To bring the idea to the next level, we need to model how the destruction of technology affects the growth of technology.

One intuition that the emergence of a new technology might depend on any technology we have created before. This reminds me of the population activity in neuroscience ².

Suppose we denote the amount of technology that appeared at time $t$ as $N(t)$, again. In general, the equation we should have is

$$ \begin{equation} N(t) = \int_{-\infty}^t K(t\vert t’) N(t’) dt’, \end{equation} $$

where $K(t\vert t’)$ is the kernel of the convolution.

This new model really covers what we have before as a simple exponential growth model. The reason is the following.

For $K(t\vert t’)\sim C\delta(t-t’)$, which means the new technology depends only on the most current appearance rate of technology, the model falls back to the exponential growth case.

We could also imagine that for a very narrow kernel, the amount of technology grows almost exponential. On the other hand, a broad kernel leads to a very wide depend on the past growth. This actually includes the effects of the economy history, as well as other possible factors. The reason is that we expect the number of technology depends on economy and we have already set the amount of technology at time $t$ to depend on the past $t’$. Destruction effect is also packed and loaded.

To find out what kind of kernel fits the data well, we probably have to guess. Meanwhile, I am starving and need some food.